Hola amigos, nuevamente estoy por aquí compartiendo nuevas experiencias acerca del curso. El blog estaba un poco abandonado, pero ya estoy de vuelta.
El día de hoy, compartiré el tema que me toco exponer en mi clase de Análisis de Algoritmos. Escogí este tema porque siempre he tenido un gusto por los grafos. El tema se titula "Caminos mas cortos desde un origen a múltiples destinos". El camino mas corto es un problema clásico en la teoría de grafos y se han propuesto un gran numero de diferentes soluciones. Por lo general, inicialmente tenemos un grafo $G=(V,E)$ donde $V$ es el conjunto de vértices de los cuales pueden representar ciudades, estados, maquinas etc. y un conjunto $E$ de aristas las cuales se le asignan ciertos pesos que representan por ejemplo, distancias entre sitios, tiempos de separación entre ciertas tareas ejecutadas, costos de la transmisión de información entre localidades, etc. El problema del camino mas corto tiene muchas variantes, desde hallar el camino mas corto a partir de un vértice fuente a un vértice destino, a hallar todos los caminos mas cortos entre cada par de vértices del grafo. En este caso el problema que discutiremos es, hallar los caminos mas cortos desde un vértice fuente a todos los demás vértices que componen el grafo.
Antes de presentar los algoritmos que nos permitirán dar una solución a este problema y dar un breve ejemplo del mismo, se mostraran algunas generalidades importantes, que debemos tener en cuenta en esta teoría...
Formalmente...
Sea un grafo dirigido $G(V,E)$ ponderado, con una función de peso
$w:E \rightarrow R$ que asigna a las arista pesos de valor real.
El peso de un camino $p=<v_{0},v_{1},...,v_{k}>$ es la suma de
los pesos de las aristas que lo componen:
$w(p)=\sum_{i=1}^{k}w(v_{i-1},v_{i})$
El peso del camino mas corto de $u$ a $v$ por
$\delta(u,v)=\left\{\begin{array}{cl}min\{w(p): \stackrel{p}{u \rightsquigarrow v}\} & \mbox{si existe un camino de u a v }\\ \infty &\mbox{otro caso}\end{array}\right.$
El camino mas corto de un vértice $u$ a otro $v$
esta definido por algún camino $p$ tal que
$w(p)=\delta(u,v)$
En otras palabras el camino de mínimo peso de $u$ a $v$
$\delta(u,v)=\left\{\begin{array}{cl}min\{w(p): \stackrel{p}{u \rightsquigarrow v}\} & \mbox{si existe un camino de u a v }\\ \infty &\mbox{otro caso}\end{array}\right.$
El camino mas corto de un vértice $u$ a otro $v$
esta definido por algún camino $p$ tal que
$w(p)=\delta(u,v)$
En otras palabras el camino de mínimo peso de $u$ a $v$
Ahora podemos definir el problema de los caminos mas cortos desde un origen a varios destinos como: Dado un grafo $G(V,E)$ nosotros queremos encontrar los caminos mas cortos desde un vértice origen $s \in V$ A cada vértice $v \in V$
Algo que caracteriza a los algoritmos para encontrar caminos mas cortos o mas largos, es el paradigma de la Programación Dinámica, y este caso no es la excepción, sin embargo para usar esta técnica debemos primero establecer la una subestructura óptima.
Subestructura Óptima para caminos mas cortos: $$Un \ subcamino \ de \ un \ camino \ corto \ es \ tambien \ un \ camino \ corto $$
Ahora tenemos la siguiente propiedad...
Desigualdad Triangular:
Para todo vértice $s, u , v \in V$, donde $s$ es una fuente
se tiene que $\delta(s,v) \leq \delta(s,u)+w(u,v)$
Hasta este punto hemos mencionado algunas generalidades que son de suma importancia para esta teoría de los caminos mas cortos.
Ahora para nuestro problema existen algoritmos que pueden dar solución a nuestro problema, uno de ellos es el algoritmo de Dijkstra y el de Bellman-Ford, donde su diferencia radica es en el grafo sobre el cual se esta ejecutando el algoritmo, ya que el de Dijkstra trabaja sobre grafos donde los pesos de las aristas todos son positivos, mas aun no tiene ciclos negativos alcanzados por $s$, a diferencia del algoritmo de Bellman-Ford que si permite pesos negativos en las aristas.
El que discutiremos el día de hoy es el algoritmo de Dijkstra el cual utiliza el método "Greedy Algorithms", y también una técnica muy interesante llamada relajación, en otro post, hablaremos un poco del Algoritmo de Bellman-Ford.
La idea principal es para el método Greedy Algorithm:
- Un conjunto $S$ de vértices cuya distancia del camino mas corto desde $s$ es conocida.
- En cada paso adicionamos un vértice $v \in V-S$ cuya distancia estimada es mínima, (este sera nuestro criterio de escogencia)
- Guardar estas distancias estimadas de vértices adyacentes a $V$
La técnica de relajación de la que hace uso el procedimiento, consiste en atribuirle a cada vértice $v \in V$ una estimación $d[]$ del peso del camino mas corto de $s$ a $v$, $d[]$ la denominaremos estimación del camino mas corto, ejemplo:
Supóngase que deseamos relajar la arista $(u,v)$ el procedimiento es el siguiente:
Previamente inicializamos, nuestro grafo con estimaciones de infinito tomando esto como que nuestro camino mas corto es muy grande, el procedimiento es el siguiente:
El método de relajación para una arista $(u,v)$
Aquí $\pi[v]$ indica el predecesor de $v$. A continuación se muestra la relajación de la arista $(u,v)$ como ejemplo...
El Algoritmo de Dijkstra es el siguiente...
En el anterior algoritmo $Q$ representa una cola de prioridad sobre las llaves guardadas y EXTRAMIN() extraerá el tamaño del camino mas corto por las condiciones de $Q$.
Aplicación del Algoritmo de Dijkstra...
Hacer una tabla con las estimaciones de los caminos mas cortos aveces resulta mas útil este es un ejemplo de cuando finaliza el algoritmo, donde los números con asterisco indican el peso del camino mas corto para llegar desde $s$ al vértice que lidera la columna:
Como ven para llegar de $s$ a $t$ tenemos un camino de peso 8, para llegar a $y$ un camino de peso 5, a $x$ de peso 9 y finalmente para llegar a $z$ un camino de peso 7.
Eso es todo amigos... nos vemos en una próxima edición.

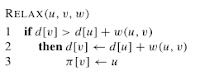




0 comentarios:
Publicar un comentario